目次
1.『ロジカルシンキング』とは

社会人になると、論理的に思考すること、つまり「ロジカルシンキング」が求められる場面が多くなります。
もう少し詳しく説明すると、ロジカルシンキングは、物事の因果関係を整理し、筋道を立てて考えることと、物事を体系的に整理することによって、矛盾が起こらないように考える思考法、と言うこともできます。
2.社会人にとって『ロジカルシンキング』は重要なスキル
たとえば、プライベートで、家族や仲の良い友人と過ごすのであれば、少しの会話からでも、相手はあなたの言いたいことを理解してくれるかもしれません。
しかし、仕事においても、上司や同僚、取引先のお客様に対して、同じような話し方をするのが、果たしてふさわしいのでしょうか?
仕事では、様々な立場や価値観の人、時には初めて会う人とも接点を持ち、自分の考えを伝え、お互いにスムーズに仕事を進められるようにしなければなりません。
その時に、ロジカルシンキングで、矛盾なく物事を整理し、相手に伝えることは、とても重要なスキルになるのです。
そこで今回は、ロジカルシンキングの代表的な思考法について確認していきましょう。
3.『ロジカルシンキング』の代表的な2つの思考法
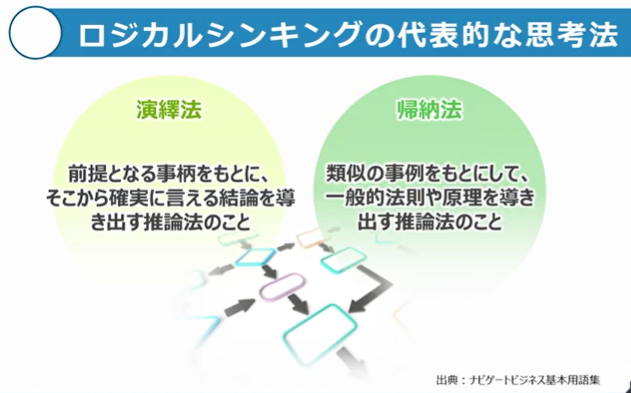
ロジカルシンキングの代表的な2つの思考法として「演繹法」と「帰納法」という考え方があります。
演繹法は、前提となる事柄をもとに、そこから確実に言える結論を導き出す推論法をさします。
一方で、帰納法とは、類似の事例をもとにして、一般的法則や原理を導き出す推論法のことを言います。
では、この2つの思考法について、さらに詳しく見ていきましょう。
4.『演繹法』
4-1. 「演繹法」とは
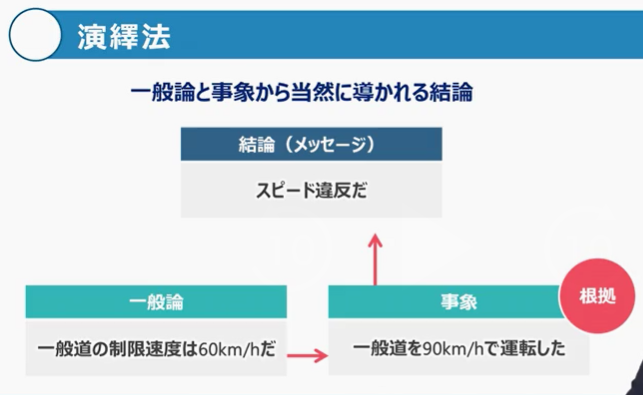
演繹法は、前提となる事柄、つまり、一般論をもとに、ある事業から結論を導き出す思考法です。
ここでは、スピード違反を例にとって、演繹法を使ってスピード違反であることの論拠を示してみましょう。
「一般道の制限速度は時速60kmだ」というルールは、一般に広く知られています。
つまり、このルールは一般論と言えます。それに対して、「一般道を時速90kmで運転した」という人がいたとします。
この時、先ほどの一般論に照らし合わせて考えてみると、「一般道を時速90kmで運転する」ことは、「スピード違反である」という主張・結論には、誰もが納得するでしょう。
このように、一般論と事象を重ね合わせて、主張に対して論理構成することを、演繹法と言います。
4-2. 演繹法の弱点
演繹法はロジカルシンキングで大切な思考法ですが、弱点もあります。
それは、相手が納得するかどうかは、相手が一般論を認識しているかどうかにかかっている、という点です。
例えば、日本に来て日が浅い外国人は、一般道の制限速度が時速60kmであることを、知らない場合があります。
そうすると、前提であるはずの一般論が成立せず、主張や結論が機能しなくなってしまうのです。
演繹法も万全ではないことを理解しておきましょう。
5.『帰納法』
5-1. 「帰納法」とは
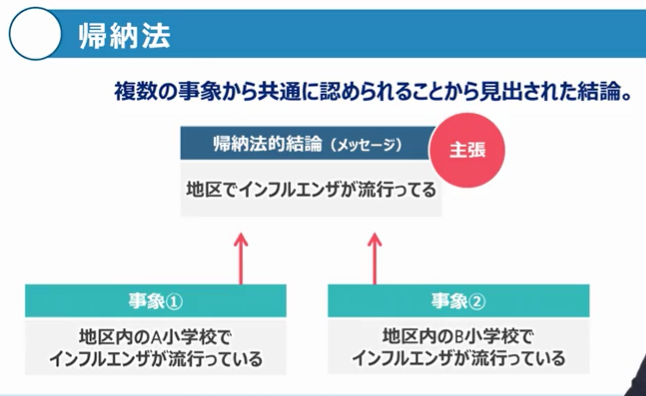
帰納法は、複数の事象に見られる共通の事実から、結論を導き出す思考法です。
例えとして、「地区でインフルエンザが流行っている」という主張を、帰納法を使って論拠を示してみましょう。
ある同じ地区内のA小学校とB小学校では、どちらもインフルエンザが流行っていたとします。
この2つの事象から、「この地区ではインフルエンザが流行っている」という主張・結論を導き出すことができます。
このように、複数の同じ事象を根拠に、論理構成するのが帰納法です。
5-2. 帰納法の弱点
帰納法にも、演繹法と同じように、弱点が存在します。
帰納法は、複数の共通事象がある、という事実だけで結論を導き出すため、注意が必要です。
例えば、先ほどのA小学校とB小学校の他に、同じ地区にはC小学校が存在しており、「C小学校ではインフルエンザが流行っていない」という事実が明らかになったとします。
そうすると、「地区ではインフルエンザが流行っている」という帰納法の根拠が弱まることになります。
5-3. 批判的検証で帰納法の確度を高める
このように、ロジカルシンキングの代表的な思考法である帰納法も、万全ではないのです。
そこで重要になるのが、批判的な検証を繰り返して、主張や結論の確度を高めることです。
批判的な検証とは、根拠から「So what? 何が言いたいのか?」と主張・結論を問うこと、逆に主張・結論から「Why True? その根拠は本当か?」と根拠を問うことです。
この2つの問いを繰り返すことで、より納得度の高い主張・結論を導き出せるでしょう。
6.論理的思考法の基礎となる『MECE』

演繹法、帰納法のような、論理的思考法を活用する際には、MECEという基本概念を頭に置いておくことが、思考を手助けしてくれます。
「MECE」とは、「Mutually Exclusive」&「Collectively Exhaustive」という英語の頭文字を取ったもので、「互いに重複がなく、全体にモレがない」という意味です。
つまり、ある集合においてモレもダブりもない、つまり、互いに排反でなく、部分の集合の和が全体の和と一致している状態です。
モレもなくダブりもなく、現状を正しく把握できている状態と言えます。
一方で、「モレなくダブりなく」が徹底できていない、例えば、ある事象と別の事象の一部が重複してしまったり、どの事象でも触れられていない部分があったりすると、現状を正しく把握できず、根拠を持って論理的に説明できていない状態と言えるでしょう。
論理的思考をするうえで、MECEはとても重要な考え方であることがわかりますね。
7.まとめ

いかがでしたでしょうか。以上のように、ロジカルシンキングでは、主張を明確にし、演繹法や帰納法などを用いて、根拠を積み重ね、批判的に検証して結論を導き出します。
その為、結論を支える根拠がMECEであることが重要です。
日頃からロジカルシンキングを意識的に心がけることで、説得力のある主張ができるようにしていきましょう。
なお、「ロジカルシンキング」コースでは、他にも、代表的なフレームワークや、ファシリテーション、プレゼンテーションなどを学ぶことができますので、ぜひ視聴してみてくださいね。
▼サンプル動画はこちら▼








